What concepts or facts do you know from math that is mind blowing, awesome, or simply fascinating?
Here are some I would like to share:
- Gödel’s incompleteness theorems: There are some problems in math so difficult that it can never be solved no matter how much time you put into it.
- Halting problem: It is impossible to write a program that can figure out whether or not any input program loops forever or finishes running. (Undecidablity)
The Busy Beaver function
Now this is the mind blowing one. What is the largest non-infinite number you know? Graham’s Number? TREE(3)? TREE(TREE(3))? This one will beat it easily.
- The Busy Beaver function produces the fastest growing number that is theoretically possible. These numbers are so large we don’t even know if you can compute the function to get the value even with an infinitely powerful PC.
- In fact, just the mere act of being able to compute the value would mean solving the hardest problems in mathematics.
- Σ(1) = 1
- Σ(4) = 13
- Σ(6) > 101010101010101010101010101010 (10s are stacked on each other)
- Σ(17) > Graham’s Number
- Σ(27) If you can compute this function the Goldbach conjecture is false.
- Σ(744) If you can compute this function the Riemann hypothesis is false.
Sources:
- YouTube - The Busy Beaver function by Mutual Information
- YouTube - Gödel’s incompleteness Theorem by Veritasium
- YouTube - Halting Problem by Computerphile
- YouTube - Graham’s Number by Numberphile
- YouTube - TREE(3) by Numberphile
- Wikipedia - Gödel’s incompleteness theorems
- Wikipedia - Halting Problem
- Wikipedia - Busy Beaver
- Wikipedia - Riemann hypothesis
- Wikipedia - Goldbach’s conjecture
- Wikipedia - Millennium Prize Problems - $1,000,000 Reward for a solution


The four-color theorem is pretty cool.
You can take any map of anything and color it in using only four colors so that no adjacent “countries” are the same color. Often it can be done with three!
Maybe not the most mind blowing but it’s neat.
Thanks for the comment! It is cool and also pretty aesthetically pleasing!
Your map made me think how interesting US would be if there were 4 major political parties. Maybe no one will win the presidential election 🤔
What about a hypothetical country that is shaped like a donut, and the hole is filled with four small countries? One of the countries must have the color of one of its neighbors, no?
I think the four small countries inside would each only have 2 neighbours. So you could take 2 that are diagonal and make them the same colour.
Looks to be that way one of the examples given on the wiki page. It is still however an interesting theory, if four countries touching at a corner, are the diagonal countries neighbouring each other or not. It honestly feels like a question that will start a war somewhere at sometime, probably already has.
In graph theory there are vertices and edges, two shapes are adjacent if and only if they share an edge, vertices are not relevant to adjacency. As long as all countries subscribe to graph theory we should be safe
The only problem with that it that it requires all countries to agree to something, and that seems to become harder and harder nowadays.
But each small country has three neighbors! Two small ones, and always the big donut country. I attached a picture to my previous comment to make it more clear.
In your example the blue country could be yellow and that leaves the other yellow to be blue. Now no identical colors touch.
You still have two red countries touching each other, what are you talking about?
Oops I meant the red one goes blue.
Whoops I should’ve been clearer I meant two neighbours within the donut. So the inside ones could be 2 or 3 colours and then the donut is one of the other 2 or the 1 remaining colour.
You’re right. Bad example from my side. But imagine this scenario:
That map is actually still quite similar to the earlier example where all 4 donut hole countries are the same. Once again on the right is the adjacency graph for the countries where I’ve also used a dashed line to show the only difference in adjacency.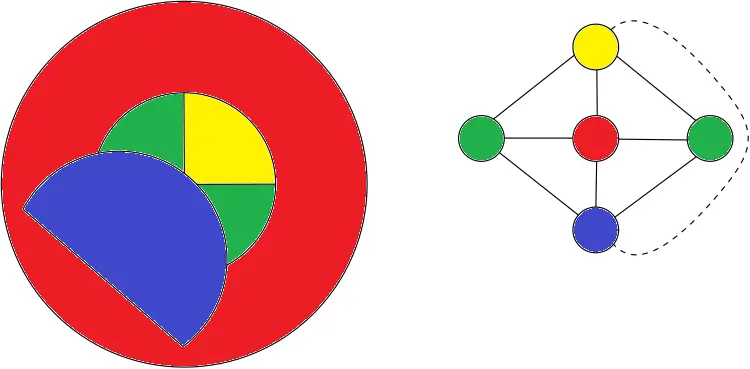
Oh wow, now I feel dumb. Thanks.
Feeling dumb is just the first step in learning something new
Make purple yellow and one of the reds purple.
…There is no purple though?
Someone beat me to it, so I thought I’d also include the adjacency graph for the countries, it can be easier to see the solution to colouring them.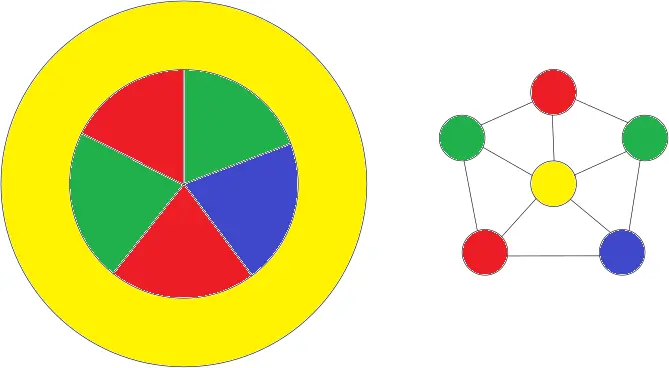
There are some rules about the kind of map this applies to. One of them is “no countries inside other countries.”
Not true, see @BitSound’s comment.
It does have to be topologically planar (may not be the technical term), though. No donut worlds.
The regions need to be contiguous and intersect at a nontrivial boundary curve. This type of map can be identified uniquely with a planar graph by placing a vertex inside each region and drawing an edge from one point to another in each adjacent region through the bounding curve.
I see.
In that image, you could color yellow into purple since it’s not touching purple. Then, you could color the red inner piece to yellow, and have no red in the inner pieces.
I read an interesting book about that once, will need to see if I can find the name of it.
EDIT - well, that was easier than expected!
Read the author as Robin Williams
Note you’ll need the regions to be connected (or allow yourself to color things differently if they are the same ‘country’ but disconnected). I forget if this causes problems for any world map.
I suspect that the Belgium-Netherlands border defies any mathematical description.
If you had a 3 dimensional map, would you need more colors to achieve the same results?
Edit: it was explained in your link. It looks like for surfaces in 3D space, this can’t be generalized.
this whole thread is the shit.
Isn’t the proof of this theorem like millions of pages long or something (proof done by a computer ) ? I mean how can you even be sure that it is correct ? There might be some error somewhere.