196@lemmy.blahaj.zoneEnglish · 3 days ago

Showing off some cool Wild Knot fractals

media.piefed.social

145

Showing off some cool Wild Knot fractals

media.piefed.social

SmokeyDope@piefed.social to

196@lemmy.blahaj.zoneEnglish · 3 days ago

A while ago I was having fun theorycrafting seeing if there were potential connections relating knot geometry/ formation to wavefunction field excitation as well as better understanding computational complexity classes of knot formation.

During my research I came across an interesting class of fractal ’ wild knots ’ that recursively cross into eachother infinitely. The wild knot shown in post displays cantor set class bifurcation.

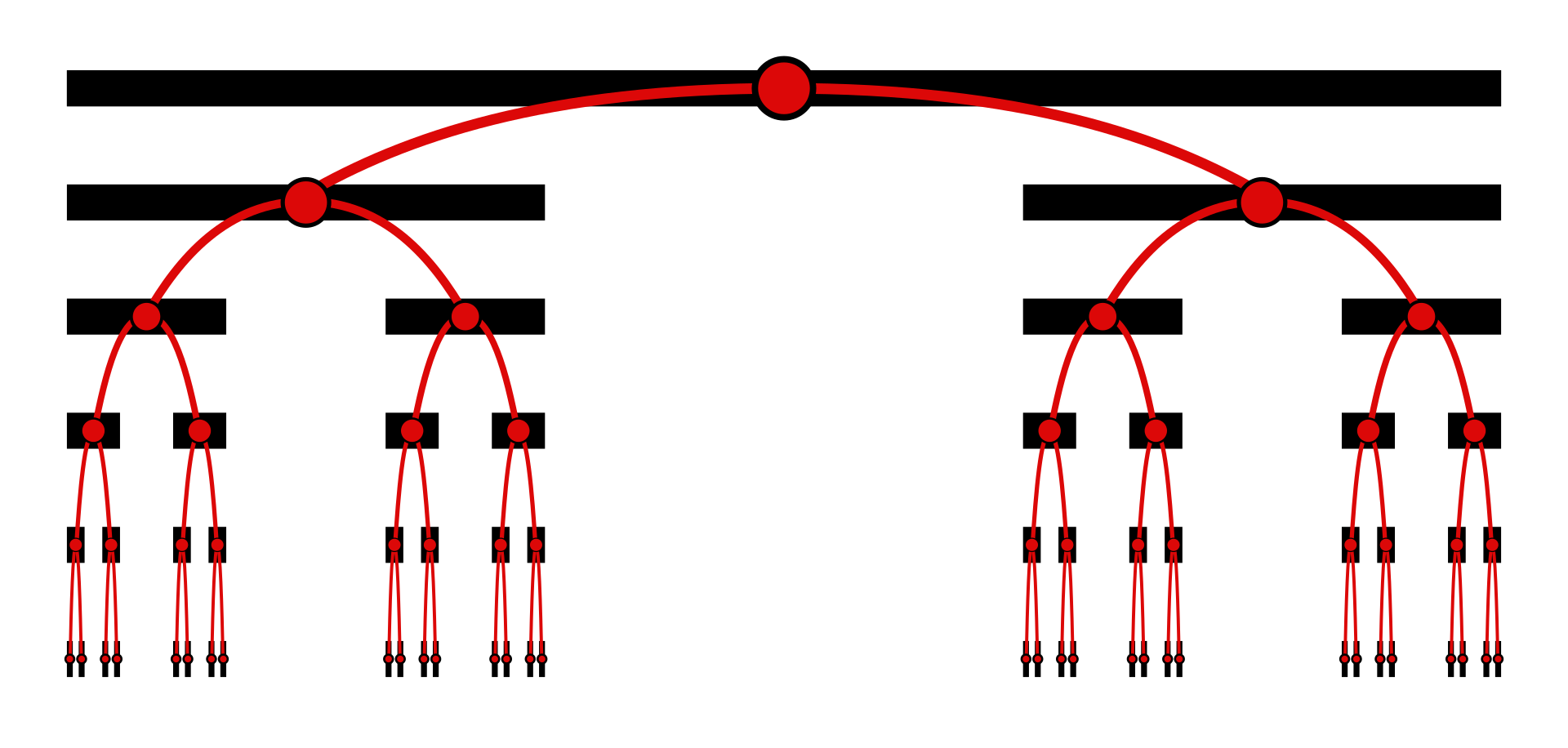
Heres a 3d animation of a knot known as the ’ Alexander Horned Sphere ’

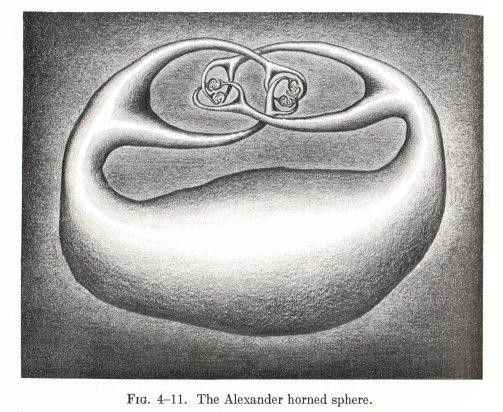
These knots are pretty cool to look at.

Chat

TriangleSpecialist@lemmy.world
link
fedilink
English
arrow-up
2·
2 days ago
You just reminded me there was a sculpture of an Alexander horned sphere in the maths lab where I did my studies. It was pretty shitty and obviously there were only a few branches. It confused the hell out of us as undergrads.

Thanks for the trip down memory lane.

196@lemmy.blahaj.zone

onehundredninetysix@lemmy.blahaj.zone

Create a post

You are not logged in. However you can subscribe from another Fediverse account, for example Lemmy or Mastodon. To do this, paste the following into the search field of your instance: !onehundredninetysix@lemmy.blahaj.zone

Community Rules

You must post before you leave

Be nice. Assume others have good intent (within reason).

Block or ignore posts, comments, and users that irritate you in some way rather than engaging. Report if they are actually breaking community rules.

Use content warnings and/or mark as NSFW when appropriate. Most posts with content warnings likely need to be marked NSFW.

Most 196 posts are memes, shitposts, cute images, or even just recent things that happened, etc. There is no real theme, but try to avoid posts that are very inflammatory, offensive, very low quality, or very “off topic”.

Bigotry is not allowed, this includes (but is not limited to): Homophobia, Transphobia, Racism, Sexism, Abelism, Classism, or discrimination based on things like Ethnicity, Nationality, Language, or Religion.

Avoid shilling for corporations, posting advertisements, or promoting exploitation of workers.

Proselytization, support, or defense of authoritarianism is not welcome. This includes but is not limited to: imperialism, nationalism, genocide denial, ethnic or racial supremacy, fascism, Nazism, Marxism-Leninism, Maoism, etc.

Avoid AI generated content.

Avoid misinformation.

Avoid incomprehensible posts.

No threats or personal attacks.

No spam.

Moderator Guidelines

Moderator Guidelines

Don’t be mean to users. Be gentle or neutral.
Most moderator actions which have a modlog message should include your username.
When in doubt about whether or not a user is problematic, send them a DM.
Don’t waste time debating/arguing with problematic users.
Assume the best, but don’t tolerate sealioning/just asking questions/concern trolling.
Ask another mod to take over cases you struggle with, if you get tired, or when things get personal.
Ask the other mods for advice when things get complicated.
Share everything you do in the mod matrix, both so several mods aren’t unknowingly handling the same issues, but also so you can receive feedback on what you intend to do.
Don’t rush mod actions. If a case doesn’t need to be handled right away, consider taking a short break before getting to it. This is to say, cool down and make room for feedback.
Don’t perform too much moderation in the comments, except if you want a verdict to be public or to ask people to dial a convo down/stop. Single comment warnings are okay.
Send users concise DMs about verdicts about them, such as bans etc, except in cases where it is clear we don’t want them at all, such as obvious transphobes. No need to notify someone they haven’t been banned of course.
Explain to a user why their behavior is problematic and how it is distressing others rather than engage with whatever they are saying. Ask them to avoid this in the future and send them packing if they do not comply.
First warn users, then temp ban them, then finally perma ban them when they break the rules or act inappropriately. Skip steps if necessary.
Use neutral statements like “this statement can be considered transphobic” rather than “you are being transphobic”.
No large decisions or actions without community input (polls or meta posts f.ex.).
Large internal decisions (such as ousting a mod) might require a vote, needing more than 50% of the votes to pass. Also consider asking the community for feedback.
Remember you are a voluntary moderator. You don’t get paid. Take a break when you need one. Perhaps ask another moderator to step in if necessary.

Visibility: Public

This community can be federated to other instances and be posted/commented in by their users.

1.75K users / day
4.16K users / week
7.58K users / month
18.1K users / 6 months
5 local subscribers
4.81K subscribers
5.68K Posts
74.6K Comments
Modlog